Distributed ML (book)
Distributed Machine Learning
Contents
[toc]
分布式机器学习框架
为什么需要分布式机器学习? - 计算量/训练数据/模型太大
主要模块:数据与模型划分、单机优化、通信以及数据与模型聚合。
数据与模型划分
数据划分
样本划分(对训练样本)
随机采样
置乱切分 - 乱序排列后顺序切分
维度划分(对每个样本的特征维度)
将这 d 维特征顺序切分成 K 份,然后把每份特征对应的子数据集分配到 K 个工作节点上
模型划分
单机优化
通信
通信内容 - 模型更新(参数),重要样本,计算中间结果(模型并行)
通信拓扑结构
AllReduce - Spark MLlib
Parameter Server - Pentuum
数据流 - TensorFlow
通信步调
同步 - BSP-SGD, 模型平均,ADMM, EA-SGD
异步 - ASGD, HogWild, Cyclades
半同步(设置延迟阈值),混合同步(组内同步,组间异步)
通信频率
最优通信频率 - 平衡计算代价和通信代价
减小带宽需求 - 模型压缩/量化
分类 - 时域滤波(降低通信频率),空域滤波(减少发送内容)
数据与模型聚合
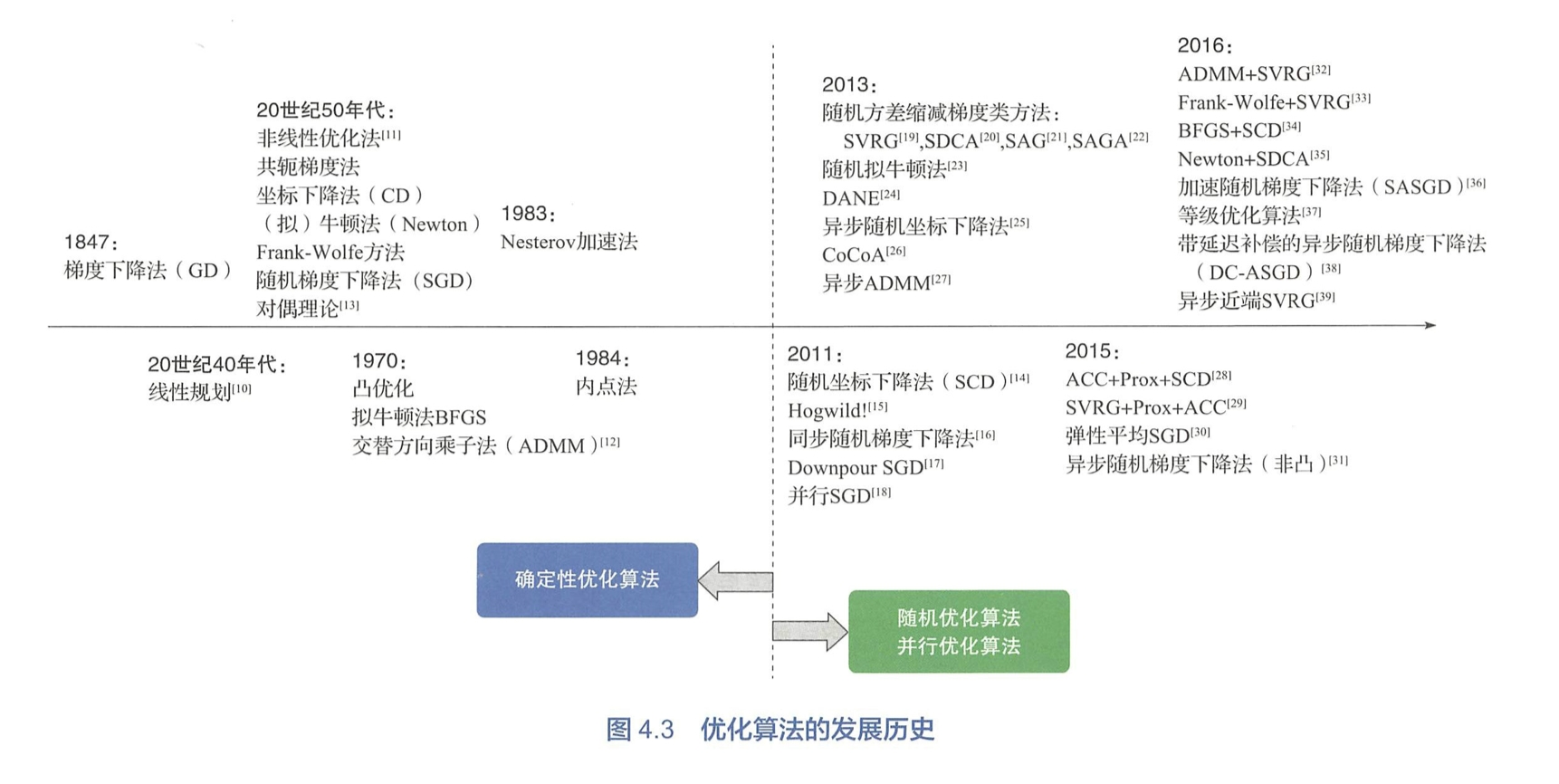
确定性优化
概述
收敛速率
线性 - $\log \epsilon(T)$与$T$同阶
次线性,超线性
特别地,二阶收敛速率 - $\log \log \epsilon(T)$与$T$同阶
凸性:R^d^上凸,强凸
强凸 $|f(w)-f(v)| \geqslant \nabla f(w)^{T}(w-v)+\frac{\alpha}{2}|w-v|^{2}$
光滑性(刻画函数变化的缓急程度)
可导:β-光滑 $|f(w)-f(v)| \leqslant \nabla f(v)^{T}(w-v)+\frac{\beta}{2}|w-v|^{2}$
不可导:Lipschitz连续
凸函数f是β-光滑的 <=> 导数是β-Lipschitz连续的。 所以, β-光滑的函数的光滑性质比Lipschitz连续的函数的光滑性质要更好(变化更加慢)。
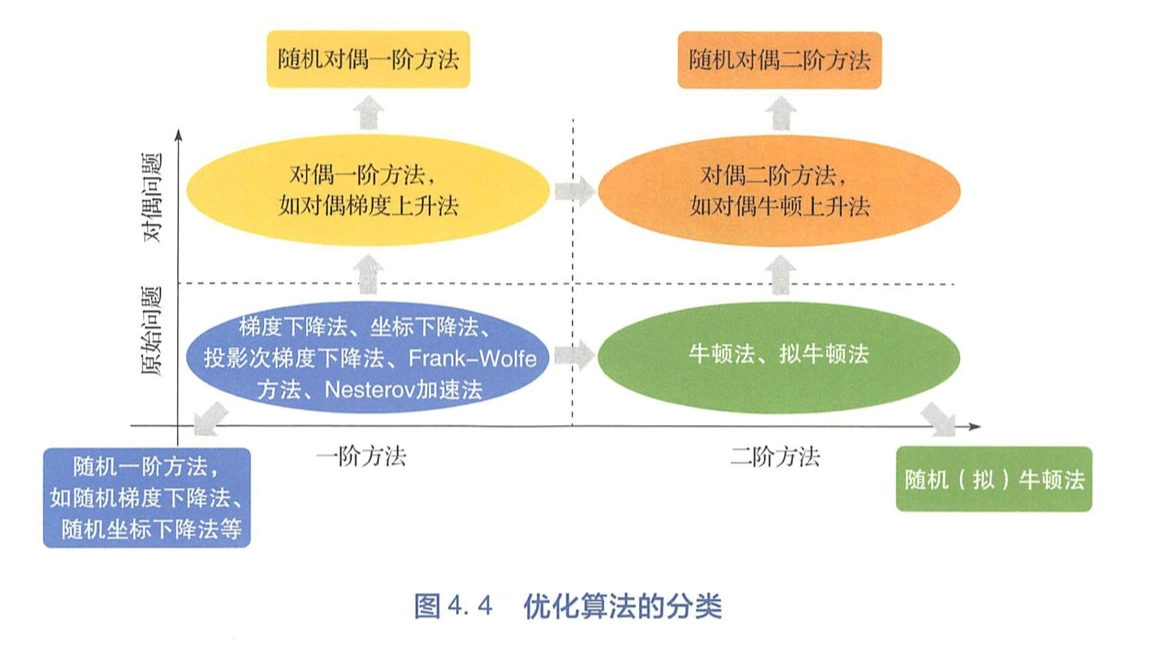
分类
是否对数据或者变量的维度进行了随机采样? -> 确定性算法 vs. 随机算法
算法在优化过程中所利用的是一阶导数信息还是二阶导数信息? -> 一阶方法 vs. 二阶方法
算法是在原问题空间还是在对偶空间进行优化? -> 原始方法 vs. 对偶方法
一阶确定性算法
梯度下降
思想 - 通过最小化目标函数当前状态的一阶泰勒展开,近似优化目标函数本身
优化性质
凸性
当目标函数是强凸函数时,梯度下降法的收敛速率是线性的 $O(1/T)$ ($f\left(w{T}\right)-f\left(w^{*}\right) \leqslant \frac{2 \beta\left|w{0}-w^{*}\right|^{2}}{T}$)
当目标函数是凸函数时,其收敛速率是次线性的 $O(e^{-T})$
即强凸性质会大大提高梯度下降法的收敛速率。进一步地,强凸性质越好(即α越大),条件数Q越小, 收敛越快 。
光滑
光滑性质在凸和强凸两种情形下都会加快梯度下降法的收敛速率,即β越小(强凸情形下, 条件数Q越小),收敛越快 。
强凸情形中的条件数和凸情形中的光滑系数在一定程度上刻画了优化问题的难易程度 。
投影次梯度下降
思想
梯度下降法有两个局限 : 一是只适用于无约束优化问题;二是只适用于梯度存在的目标函数。 投影次梯度下降法可以解决梯度下降法的这两个局限性。
利用次梯度,先梯度下降再进行投影
对于光滑函数, 在凸和强凸两种情形下, 投影次梯度下降法的收敛速率与梯度下降法相同 。
对于 Lipschitz 连续函数,投影次梯度下降法收敛,并且收敛速率在凸和强凸两种情形相比于光滑函数显著降低, 都是次线性的 。
近端梯度下降
思想 - 近端梯度下降法是投影次梯度下降法的一种推广, 适用于不可微的凸目标函数的优化问题。
收敛速率 - 强凸光滑时 $O(e^{-T/Q})$
Frank-Wolfe
投影次梯度下降法的另一个替代算法(为了解决投影计算的瓶颈)
在最小化目标函数的泰勒展开时就将约束条件考虑进去 , 直接得到满足约束的近似最小点
为了使算法的解更稳定, Frank - Wolfe 算法将求解 上述子问题得到的解与当前状态解做线性加权
Frank- Wolfe算法的收敛速率和投影次梯度下降法的相同, 可根据问题中的投影计算是否困难, 在两种算法中选择一种使用 。
一阶优化方法的收敛速率下界
在 Lipschitz 连续的条件下, 一阶算法的收敛速率的下 界与梯度下降法的收敛速率相同,说明梯度下降法已经达到了可能的最快收敛速率。然而对光滑函数,一阶方法的收敛速率的下界小于梯度下降法的收敛速率。
Nesterov 在1983 年对光滑的目标函数提出了一种加快一阶优化算法收敛的方法。可以达到光滑目标函数的一阶方法的收敛速率下界
坐标下降
梯度下降(样本采样 ) -> 坐标下降(维度采样)
二阶确定性算法
牛顿法
思想 - 梯度下降(一阶泰勒展开)-> 牛顿法(二阶泰勒展开)
牛顿法提供了更为精细的步长调节, 即利用当前状态海森矩阵的逆矩阵 。 因为步长更为精细,牛顿法的收敛速率比梯度下降法的收敛速率显著加快,具有二次收敛速率 $O(e^{-2^T})$
拟牛顿法
牛顿法问题 - 在每个时刻都需要计算当前状态的海森逆矩阵,计算量和存储量都显著增大;②海森矩阵不一定是正定。为了解决这两个问题,人们提出了拟牛顿法。
思想 - 构造一个与海森矩阵相差不太远的正定矩阵作为其替代品。此外,拟牛顿法可以迭代更新海森逆矩阵,而不是在每一时刻都重新进行逆矩阵的计算 。
拟牛顿法变种(不同的海森矩阵近似和约束条件)- BFGS, DFP, Broyden, SR1
对于强凸光滑的目标函数
一阶方法具有线性收敛速率,二阶方法具有二次收敛速率
Nesterov 加速法将梯度下降法速率中关于条件数的阶数进一步改进
投影次梯度法和 Frank- Wolfe 方法都可以用于解决带有约束的优化问题,两种方法的收敛速率相同,具体可以依据投影操作的难易程度来选择
一些拟牛顿法(比如 BFGS 算法)也可以和牛顿法一样达到二次收敛速率。
对偶方法
某些时候,如果把原始优化问题转化成对偶优化问题会更容易求解 。 比如 ,当原始问题的变量维度很高,但是约束条件个数不太多时,对偶问题的复杂度(对偶变量的维度对应于约束条件的个数)会远小于原始问题的复杂度,因而更容易求解。这也是支持向量机方法高效的主要原因。
随机优化
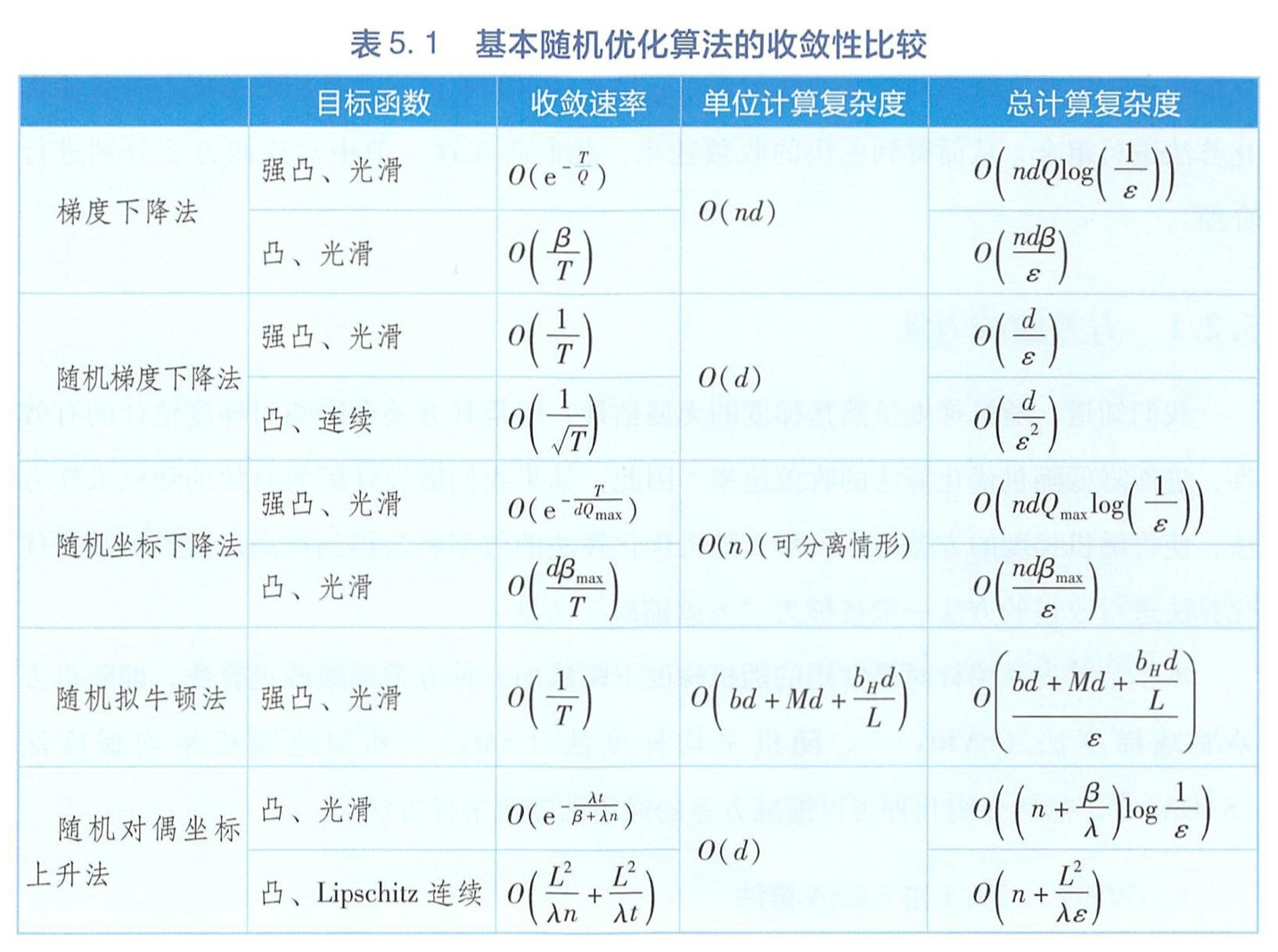
基本随机优化
结论
当数据量较大时 ,随机梯度下降法比梯度下降法更高效
如果目标函数是可分离的,随机坐标下降法比梯度下降法更高效
如果目标函数是可分离的 ,并且数据维度较高,随机坐标下降法比随机梯度下降法更高效
随机拟牛顿法的效率与随机梯度下降法的效率相同
改进
改进方向
方差缩减 - 通过缩减随机优化算法中的方差来提高对数据的利用率(随机梯度是无偏估计,但方差影响收敛速率)
算法组合 - 在基本的随机优化算法的基础上与其他优化算法进行组合,从而得到更快的收敛速率。
方差缩减
对SGD - 随机方差缩减梯度法SVRG,随机平均梯度法SAG,和加速随机平均梯度法SAGA
思想
利用了全梯度的信息对随机梯度加入正则项,得到的正则随机梯度的方差会小于原始随机梯度的方差。
正则化之后的梯度的方差会随着算法的进行逐渐收敛到0,而原始的随机梯度的方
差则不具有这个性质 。 正是由于这一良好性质,方差缩减的随机梯度法的收敛速率可以
从次线性提高到线性
可以缩减方差的通用的随机采样方法
小批量采样
带权重采样
采样所服从的概率是与各个样本所对应的损失函数的光滑系数成正比
类似地,抽取到第 j 个维度的概率与第j个维度的光滑系数冉成正比(这是Allen Zhu做的?)
此时随机梯度不再是全梯度的无偏估计,但可以降低随机梯度的方差
算法组合
随机方差缩减梯度法SVRG(次线性 -> 线性)、 Nesterov加速法(多项式阶加速)以及随机坐标下降法(保持线性收敛速度同时减小每轮计算复杂度) + X
非凸随机优化
一般来说,非凸问题的全局优化是 NP-hard问题
模拟退火,贝叶斯优化等适用于低维非凸优化问题。
连续空间中基于梯度的优化算法绝大多数只适用于凸问题,前面介绍的一阶算法、二阶算法、对偶算法,收敛 速率的保障都要求优化目标是凸的。
尝试
从已有的随机凸优化算法中,选取更适合神经网络的方法,比如 Ada 系列算法
刻画凸优化算法在非凸问题中相对于局部最优模型的收敛性质,并研究神经网络模型的局部最优模型和全局最优模型的差异
如果凸优化算法可能陷入鞍点,改进算法以逃离鞍点
设计适用于神经网络的非凸优化算法,如等级优化算法
Ada系列
实际应用中多用随机一阶方法优化NN
数据规模大,随机减少每次迭代复杂度
海森矩阵代价太大;在随机版本中, 二阶算法相对一阶算法的优势并不明显
神经网络是高度非线性的,描述其对偶问题比较困难
坐标法相对于梯度法不利于反向传播
随机一阶方法的改进
更新模型时不只利用当前的梯度,还利用历史上所有的梯度信息,并且自适应地调整步长,即Ada系列
包括带冲量SGD(最基本的Ada), AdaGrad, RMSProp, AdaDelta, Adam等
带冲量SGD
想法 - 对所有历史梯度依据其远离当前时间的程度乘以指数递减的权重, 一起决定下一步模型的更新方向 。 具体实现中引入一个辅助变量v~t~来记录历史信息,
带冲量的随机梯度下降法与 Nesterov 加速法的区别在于,前者利用在 w~t~处的梯度进行更新,后者利用在 w~t~ + µv~t~ 处的梯度进行更新 。 因而带冲量的随机梯度下降法的实现更简单
AdaGrad - 除了对历史信息(梯度值的平方)进行累加外,还根据历史梯度的大小逐维调整步长,使得梯度比较小的维度有更大的步长。照顾到一些目前梯度较小但是对搜索路径具有重要贡献的维度。
RMSProp - 与 AdaGrad 类似,区别在于它还借鉴了带冲量的随机梯度下降法的思想对历史信息进行指数递减平均
AdaDelta - 在RMSProp的基础上进一步对累加的历史信息依据梯度大小进行了调整
Adam
另一种逐维进行自适应调整步长的算法。 Adam 同时引入了以下两个辅助变量分别按照指数衰减形式来累加梯度与梯度的平方
Adam 结合了带冲量的随机梯度下降法、 AdaGrad 、 RMSProp 和 AdaDelta 等算法中所有的因素: ①更新方向由历史梯度累计决定;②对步长利用累加的梯度平方值进行修正;③信息累加按照指数形式衰减 。 因而, Adam 算法的效果最好,目前在神经网络的训练中应用最为广泛 。
非凸理论分析等 - TODO
并行
计算并行
模式 - 共享内存(如多线程)
(同步)并行执行的随机梯度下降法每次依据 K 个(来自不同 工作节点 的)样本上的梯度来更新模型, 其实等价于批量大小为 K 的小批量随机梯度下降法 。 如 果每个节点本身已 经在执行批量大小为 b 的小批量 随机梯度下降法, 则同步并行的效果相当于批量大小为 bK 的小批量随机梯度下降法。
在线/离线并行SSGD的后悔度,收敛速率
数据并行
模式 - 将数据划分后分配到各个工作节点上
样本划分 - 各算法收敛速度
维度划分 - 很多时候维度梯度高度耦合,不利于划分,但也有决策树和线性模型等对维度的处理相对独立可分的情形
模型并行
线性模型
神经网络(横向按层,纵向跨层)
通信
加速比性能定律
固定计算负载 - Amdahl定律(悲观估计)
随着处理器数目的无限增大,并行系统所能达到的加速上限为1/f(串行分量比例)
串行分量越大,并行额外开销越大,则加速越小
可扩放问题(精度)- Gustafson定律(乐观估计)
随着处理器数目的增阿基,加速几乎与处理器数目成正比,f不再是瓶颈
受限于储存器 - Sun-Ni定律(一般化)
实际应用中可供参考的加速经验公式 $p/\log p \le S \le p$
几乎无通信开销 - 矩阵相加,内积 - p
分治类 - p/log p
通信密集型 - $S = 1/C(p)$
超线性 - 剪枝
通信内容
通信主要内容 - 参数更新(数据并行),计算中间结果(模型并行)
其他内容 - 重要样本,样本预测值(与集成学习结合)
通信的拓扑结构
拓扑结构分类 - 物理拓扑结构,逻辑拓扑结构
早期 - MPI(节点间仅支持同步计算),MapReduce
发展 - 异步通信,计算和通行的统一抽象(数据图模型)
Iterative MapReduce/AllReduce
IMR - Spark MLlib, SystemML, REEF
AllReduce - MPI
共同 - 仅支持同步通信,各节点接口调用逻辑统一
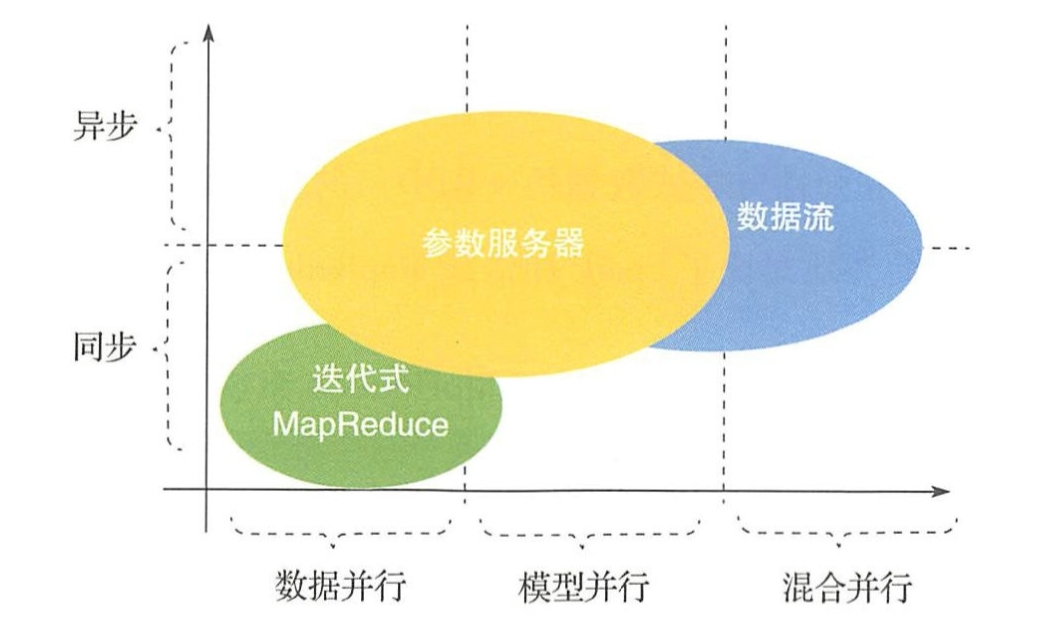
Parameter Server
结构没什么好说的...
工作节点间无需通信,仅需和服务器节点(一个或多个)通信
灵活,可以同步/异步/结合
Data Flow
上面例子各节点工作逻辑一致(接口统一),比较适合数据并行
数据流每个工作节点有两个通信通道 - 控制消息流,计算数据流
宽泛概念,IMR和PS都可以用数据流图表达
通行步调
同步通信
部分计算资源闲置(系统劣势),但模型一致,便于分析调试(算法优势)
设置全局同步屏障
异步通信
无需等待,资源利用率高,但各节点模型不一致,存在延迟
参数更新存在延迟,模型聚合变得麻烦
多线程异步通行 - 上锁时间长,为改进提出了Hogwild!(无锁异步)
同步和异步的平衡
例子 - 延时同步并行(Stale Synchronous Parallel , SSP),控制最快和最慢节点之间相差的迭代次数不超过预设的阈值
另一个想法 - 不要求最快的工作节点进行等待,而是维持一个全局时钟,当发现某些工作节点的更新太陈旧时,就将其丢弃并将此工作节点的当前模型刷新成参数服务器上的最新模型。 这样就既能保证有限的延迟,同时也可以让快的工作节点全速前进
通行频率
在本节中我们把通信频率分为时间频率和空间频率两种。其中时间频率主要指通信的频次间隔,而空间频率主要指通信的内容大小。相应地,优化通信频率可以从两方面进行,即时域滤波和空域滤波。
时域滤波
采用时域滤波的主要方法
增加通信间隔 - 会导致模型不一致,收敛性在凸情形下有保证,但NN非凸
非对称的推送和获取
例如如果某个工作节点在训练过程中本地模型参数发生的变化不太大,实际上是没有必要那么频繁地把很小的更新发送到参数服务器的 。 同样,也没有必要在每一步都对本地模型进行校准 。
平衡系统性能和模型精度
计算和传输流水线
将一次迭代分为计算和通信两个步骤。虽然相邻两次迭代之间存在依赖性,但我们可以利用机器学习的容错性,适当打破这种依赖关系,从而将两次迭代之间的计算和通信用流水线的方式并行起来。
即重叠模型的训练时间和通信时间。使用较广泛。
空域滤波
减少通信数据量 - 过滤,压缩,量化
模型过滤 - 去掉不重要的参数
如果一次迭代中某些参数没有明显变化, 便可以将其过滤掉减少通信量。
原因 - 训练后期模型参数区域收敛,只需要保留少量的参数更新信息, 整个模型学习的结果就可以有效地保留下来
按比例过滤参数 - 平衡效率和精度
模型低秩化处理 - 低秩分解压缩参数
例如用SVD将原来比较大的参数矩阵分解成几个比较小的矩阵的乘积
额外计算开销,需要权衡
模型量化 - 控制精度
模型聚合
基于模型加和
最常见
基于全部模型加和的聚合
MA(最简单),BMUF(MA上加入冲量,维护单机算法中冲量的作用),ADMM(通过解全局一致性的优化问题),SSGD(参数平均换成梯度平均),EASGD(加和工作节点和服务器模型,平衡探索新模型和历史状态)
基于部分模型加和的聚合
全部模型加和是同步并行,部分模型加和的极端就是异步
带备份节点的同步随机梯度下降法
对straggler启用额外备份节点形成竞争,空间换时间
接待近数目大时,不如异步,但类似同步方便调节精度
异步ADMM算法 - TODO
去中心化方法 - D-PSGD,可以实现线性加速比,效率比中心化方法高(通信代价小很多)
基于模型集成
模型加和最适用于凸优化,NN非凸也可以将就着用,但参数平均后性能无法保证。此节为解决此问题。
比较新的一个领域
基于输出加和的聚合
NN的损失函数关于模型参数是非凸的,但是它关于模型的输出一般是凸的
利用损失函数的凸性可以得到 $l\left(\frac{1}{K} \sum{k=1}^{K} g\left(w^{k} ; x\right), y\right) \leqslant \frac{1}{K} \sum{k=1}^{K} l\left(g\left(w^{k} ; x\right), y\right)$
即对局部模型的输出进行平均 预测结果要好于局部模型预测结果的平均值
这种对模型输出进行加和或平均的方法称为模型集成
和集成学习简直一模一样,提升精度但参数量变成K倍
模型压缩 - 如知识蒸馏
在知识蒸懵中,首先使用大规模的集成模型对样本进行再标注,然后指定一个小规模的模型,按照样本的输入特征和新的标注信息训练小规模模型中的参数。 也就是说,将大规模模型所包含 的“知识”在样本标签相同的意义下 “蒸锢” 到了小模型之中。
基于投票的聚合
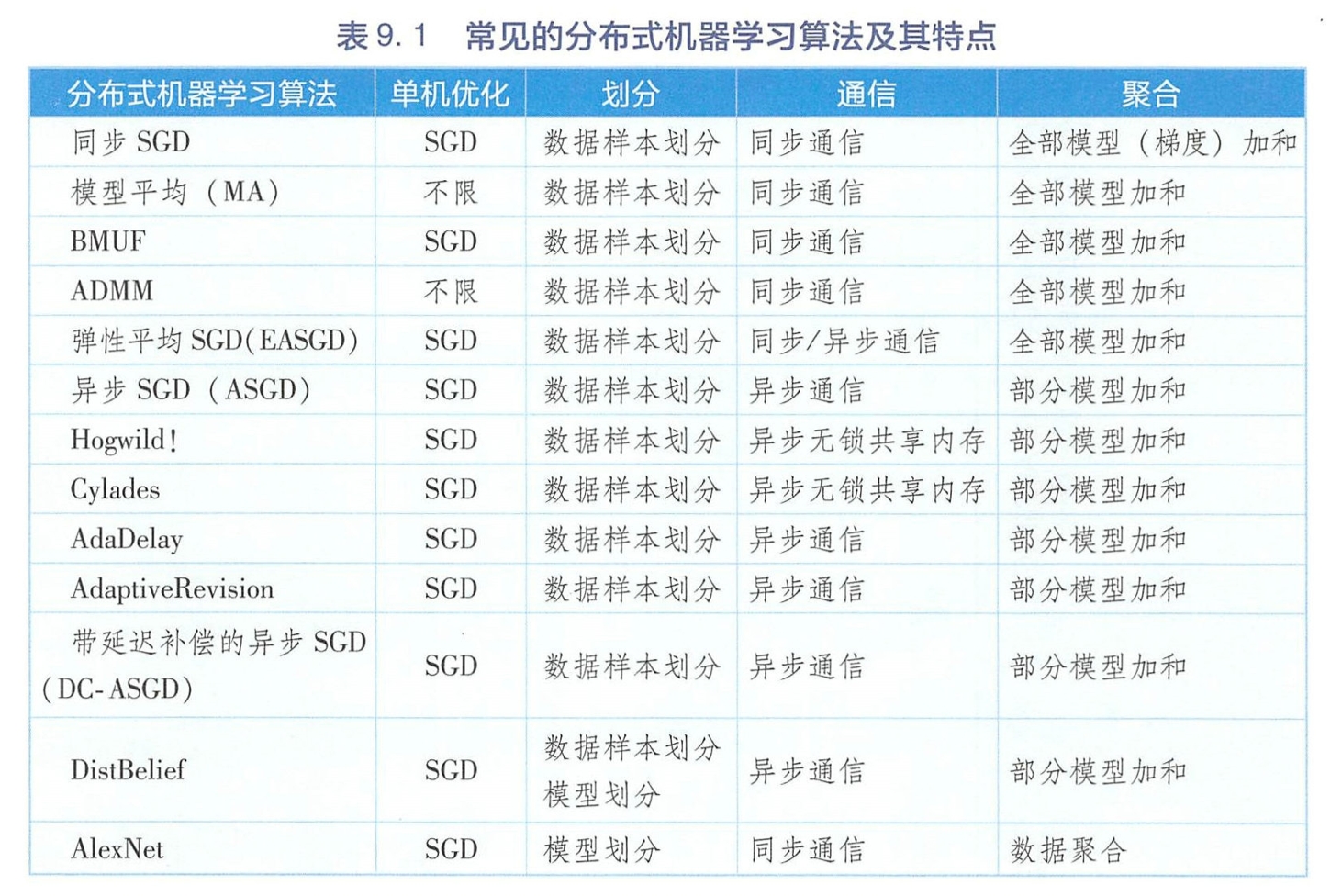
分布式机器学习算法
本章侧重 - 单机优化算法方面, 我们偏重随机梯度下降法(SGD);在数据/模型划分方面,我们偏重基于数据划分的并行算法;在模型聚合方面,我们主要讨论基于模型加和的聚合方法 。
同步算法
异步算法
同步与异步的对比与融合
模型并行
分布式机器学习理论
收敛性
加速比
泛化分析
分布式机器学习系统
迭代式MapReduce
IMR相比于传统 MapReduce增加了对迭代操作和内存管理的支持
参数服务器
略.
数据流
Last updated